E.E. Índia Vanuíre
Disciplina: Matemática –
Prof. (a): Vanessa Ribeiro de Lima
Ano/Série: 3º- Turma
A,B,C,D e E
Data:11/04/2020 a 15/04/2020
Aulas: 06
Conteúdo/Tema:
Estatística
Medidas de tendência
central: média, mediana e moda
Objetivo (s): Relacionar
informações veiculadas em diferentes fontes e com diferentes linguagens; Estabelecer
critérios sobre procedimentos estatísticos e analisar a confiabilidade acerca
das medidas envolvidas.
Habilidade (s): Saber
calcular e interpretar medidas de tendência central de uma distribuição de dados:
média, mediana e moda
Estratégia: Assistir a
aula do centro de mídias sp, https://www.youtube.com/watch?v=ebbqcThdliI&t=2073s
copiar e resolver no caderno os exercícios proposto , duvidas a esclarecer
entre em contato no meu e-mail vanessaribeirolima@prof.educacao.so.gov.br ,
mensagem pelo Facebook ou no grupo de
WhatsApp da sala
ESTATÍSTICA BÁSICA
Média aritmética simples
(Ma):
é o resultado da soma de todas as informações de um conjunto de dados dividida
pelo número de informações que foram somadas.
Exemplo: Calcule a média
anual de Carlos na disciplina de Matemática com base nas seguintes notas
bimestrais: 1ºB = 6,0;
2ºB = 9,0; 3ºB = 7,0; 4ºB
= 5,0
Média
ponderada (Mp): é calculada
multiplicando cada valor do conjunto de dados pelo seu peso. Depois,
encontra-se a soma desses valores que será dividida pela soma dos pesos.
Exemplos: João
participou de um concurso, onde foram realizadas provas de Português,
Matemática, Biologia e História. Essas provas tinham peso 3, 3, 2 e 2, respectivamente.
Sabendo que João tirou 8,0 em Português, 7,5 em Matemática, 5,0 em Biologia e
4,0 em História, qual foi a média que ele obteve
Moda
(Mo):
é
chamado de moda o dado mais frequente (que mais se repeti) de um conjunto.
Exemplos:
Em uma sapataria durante um dia foram vendidos os seguintes números de sapato:
34, 39, 36, 35, 37, 40, 36, 38, 36, 38 e 41. Qual o valor da moda desta
amostra?
Solução:
Observando
os números vendidos notamos que o número 36 foi o que apresentou maior
frequência (3 pares), portanto, a moda é igual a:
Mo
= 36
Quando
uma sequência possui mais de uma moda
Quando
procuramos o valor mais frequente dentro da sequência 12, 20, 56, 34, 15, 5, 7,
12, 5, percebemos que tanto o número 12 quanto o número 5 se repetem duas
vezes. Sem problemas! Isso significa que a sequência é bimodal, ou seja, possui
duas modas. Algo semelhante ocorre com a segunda sequência, 1, 9, 2, 1, 4, 6,
5, 3, 2, 9. Nela, os números 1, 2 e 9 são os valores mais frequentes. Assim,
podemos dizer que a sequência é trimodal.
Mediana
(Me):
representa o valor central de um conjunto de dados. Para encontrar o valor da
mediana é necessário colocar os valores em ordem crescente ou decrescente.
Quando
o número elementos de um conjunto é par, a mediana é encontrada pela média dos
dois valores centrais. Assim, esses valores são somados e divididos por dois.
Exemplo:
Em
uma escola, o professor de educação física anotou a altura de um grupo de
alunos. Considerando que os valores medidos foram: 1,54 m; 1,67 m, 1,50 m; 1,65
m; 1,75 m; 1,69 m; 1,60 m; 1,55 m e 1,78 m, qual o valor da mediana das alturas
dos alunos?
Solução
Primeiro
devemos colocar os valores em ordem. Neste caso, colocaremos em ordem
crescente. Assim, o conjunto de dados ficará:
1,50;
1,54; 1,55; 1,60; 1,65; 1,67; 1,69; 1,75; 1,78
Como
o conjunto é formado por 9 elementos, que é um número ímpar, então a mediana
será igual ao 5º elemento, ou seja:
Me
= 1,65 m
Calcule
o valor da mediana da seguinte amostra de dados: (32, 27, 15, 44, 15, 32).
Solução
Primeiro
precisamos colocar os dados em ordem, assim temos:
15,
15, 27, 32, 32, 44
Como
essa amostra é formada por 6 elementos, que é um número par, a mediana será
igual a média dos elementos centrais, ou seja:
1)
Em
cada caso, calcule a média aritmética os valores:
a)
23-20-22-21-28-20
b)
7-9-9-9-7-8-8-9-9-9
c)
0,1-0,1-0,1-0,1-0,2-0,2
d)
3-3-3-3-3-3-3-3
2)
Em
um edifício residencial com 54 apartamentos, 36 condôminos pagam taxa de
condomínio de R$ 270,00; para os demais, essa taxa é de R$ 360,00. Qual é o
valor da taxa média de condomínio nesse edifício?
3)
Um
time de futebol realizou algumas partidas e os resultados foram 3 a 1, 4 a 2, 1
a 1, 0 a 0, 3 a 2, 2 a 1 e 1 a 0. Sabendo que o time não perdeu nenhuma
partida, calcule a média aritmética dos gols:
a) marcados b) sofridos
4)
Qual
é a média de idade de um grupo em que há 6 pessoas de 14 anos, 9 de 20 anos e 5
de 16 anos?
5)
De
segunda-feira a sábado, os gastos com alimentação de uma pessoa foram 15, 13,
12, 10, 14 e14 reais. Determinem a média diária de gastos (Ma) e a mediana (Me).
6)
Considerando
os números 126, 130, 126 e 102, calculem:
a) a média aritmética (Ma);
b) a média aritmética ponderada (Mp),
com pesos 2, 3, 1 e 2, respectivamente;
c) a mediana (Me);
d) a moda (Mo).
7)
Uma
prova com 5 questões foi aplicada em uma turma. O levantamento estatístico dos
acertos foi registrado no gráfico abaixo:
Determinem a partir do gráfico:
a) o número de alunos da turma;
b) a porcentagem da turma que acertou as 5 questões;
c) a porcentagem da turma que acertou 3 ou mais questões;
d) a Ma, a Mo e a Me de acertos por pessoa
8)
Determinem
a Ma, a Mo e a Me a partir das tabelas de frequências.
![Blog da Escola Índia Vanuíre - [Ensino Médio]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgkmFtDGvKKu742xlJ2VSBZOw38wWgXfOWgAgM_lc6yjiY-CV4_sjD7kIBc-JQMTdAjz3ROBwDUoG5P6ryZAlJ5XQq4DrOaUmzqXv0rKjemH8upAdcs_nzJ8Oy3ZeoCWe8ZDxqqaVb5eZE/s1600/BA.jpg)
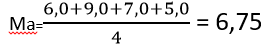




Sem comentários:
Enviar um comentário